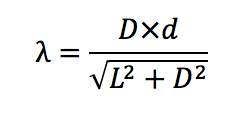d= 2*10^-6 m = 500 slits per mm
D= distance of the light spectra
L= 0.97 ± 0.005 m
as you can see it is really hard to point at a position with high precision for D. That is the reason we end up getting a huge uncertainty to compensate for the measurement difficulties.
Next is the table for λ and its associated voltage and the graph of voltage vs 1/λ.
±0.001 ±42767
The horizontal axis on the graph is the 1/λ and the vertical is the voltage.
Using the following formula we calculated the planks constant:
where e is charge of an electron and V is the voltage measured across the LED by a meter and finally c is the speed of light.
e = 1.602E-19
c=3E8
The values calculated from measurement all agree with h within uncertainty. However the most amount of error is associated with green and yellow which as mentioned before might be due to the fact that while we were looking through the grating the least resolved and sharp light lines were from green and yellow and that is why they are both from the actual value by 7 and 10 percent respectively.